Vectors and Scalars

Position, velocity, and acceleration are key to understanding motion. To know that something moved, we need to know position. To understand in what way something moved, we need to know velocity and acceleration.

To put it plainly, you will have no idea where I am if I simply say, “I moved at three miles an hour”. Even if we assume that I walk in a straight line and never stop to smell the roses, to know where I end up on my little walk you need to know more than just the speed at which I am moving and the duration of my walk. Those are just numbers, and while numbers are very real and useful, we have no reliable way to map them onto the real world and find where my walk ended.

It may sound pedantic (and I agree that physicists can be extremely nit-picky about what look like silly symbols), but we need not only numbers, but also something which can be defined according to geometric principles. We need numbers to say, “I have twice as much cheese as Sharon”, and we need geometric objects to say, “the plane flew at 100 knots with a heading of 150◦ (South-East)”.

Scalars, for now, can mostly be thought of like numbers, while vectors are geometrical objects.

Scalars

Scalars are quantities that have magnitude [1, p 1]. For example, temperature is a scalar, since it’s only defining feature is a magnitude; “it’s 30◦F”, “it’s 100◦C”. Mass would also be a scalar. So would speed.

Scalars are multiplied, divided, added and subtracted in ways which you are most likely familiar; you can think of them just like the numbers you might use in an arithmetic or algebra class. For the scalars a = 10 and b = 20,

Thinking about the real world, cars are equipped with speedometers. This device indicates how fast the car is moving. It doesn’t, however, indicate in what direction the car is moving. So a speedometer gives a number which is a scalar.

Vectors

The true horror of adulthood isn’t taxes or back pain - it’s the day you catch yourself passionately debating optimal traffic routes. Any sane driver will disregard our sophisticated calculations to follow a GPS app even if it plotted a trajectory straight through a brick wall. Yet we persist. This very human tendency to break down directions into their component parts actually mirrors how we work with vectors in mathematics.

You could describe me as a human female - which is helpful enough unless you’re trying to find me in a crowd at a Taylor Swift concert. In the same way, a vector is simply a mathematical object with direction and magnitude. Sure, there’s more to both of us than that, but it’s a start!

Picture this: you’ve just launched a rubber chicken from a cannon. Our heroic, honking bird isn’t just flying - it’s demonstrating vector physics through its velocity. This velocity is a vector because it can be broken apart according to geometric principles [1, p 2-3]; thus, we call vectors geometrical objects. This majestic bird has three possible directions of travel: forward/back (x), side-to-side (y), and up/down (z). If you shoot it straight up like a feathered rocket, it’s moving up and down in the z direction only, and (much like my yodeling career) it is not moving forward at all. The chicken’s total velocity is all these directions

added together, which we can write as:

or, as people usually write these as components,

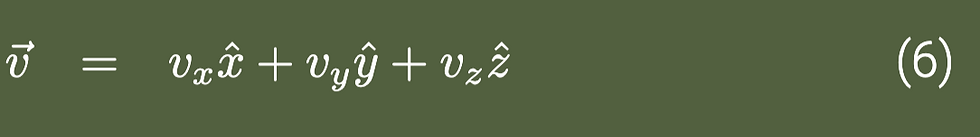
where v_x, v_y , and v_z are scalar quantities [1, p 5].

This is different from the magnitude of the velocity, which is obtained in the same way we use the pythagorean theorem; by squaring the components and then taking the square root of their sum [1, p. 5].

Vector Addition/Subtraction

You already know how to add and subtract scalars, but now vectors have multiple axes which are independent of each other. In physics, mixing vector components is like trying to marry into four royal families at once - it’s chaotic, messy, and will ultimately lead to a beheading. To avoid such a fate, we need to add like components. For example,

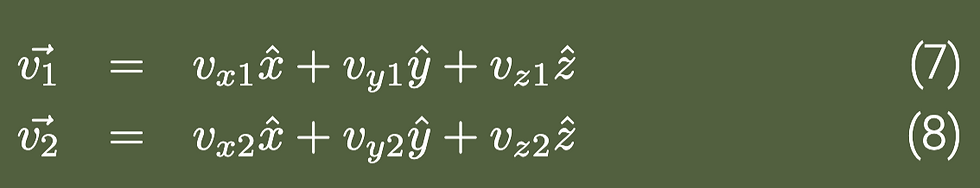
These two vectors combine as

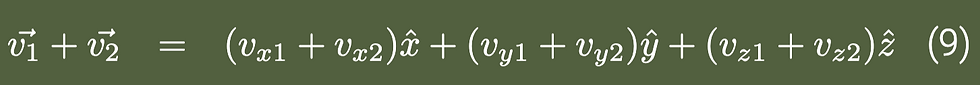
or as

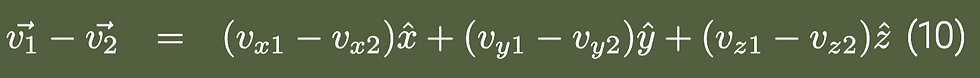
[1, p. 5].

Vector Multiplication

Vector multiplication, on the other hand, is like medieval matchmaking - there are several ways to do it and even more ways to do it wrong, but you are technically married in the end. At the present, it’s not really important to define everything precisely, because that is not only overwhelming, but simply not helpful. So I will describe two primary methods for multiplying vectors: The dot and cross products.

Dot Product

The dot product is called so because it is written as

with a little dot between the two vectors that are being multiplied. This essentially means that (similar to vector addition) each component of one vector is multiplied by it’s respective component in the other vector [1, p. 14][2, p. 235].

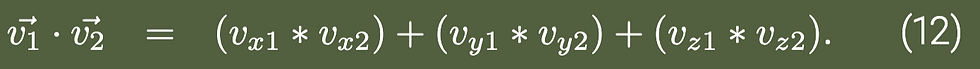
Another way to write this dot product is by multiplying the magnitude of each vector and then multiplying the result by the cosine of the angle between them.

[2, p. 235].

Cross Product

The cross product is quite a different way to multiply vectors. Here we say,

[1, p 21][2, p 238].

Another way to write this cross product is by multiplying the magnitude of each vector and then multiplying the result by the sine of the angle between them.

[2, p. 236].

Vector Division Isn’t Possible

Strange as it sounds, it is not possible to divide vectors. This boils down to a uniqueness issue. If I say, “what is ten divided by two?”, then you might easily answer me by saying, “five, of course.” Now imagine that there was another person in the room who said, “four.”. Because we know that one of you is correct, we also know that the division of scalars (plain numbers) satisfies uniqueness. Consider the following problem which uses scalars:

and therefore

Does it make much sense for 10/5 to equal 2, 6, 9, 5, or any other number of answers? No. Unlike scalars, if we try to divide one vector by another we could end up with multiple possible answers. As we have just determined, there are multiple ways to multiply vectors. Those various methods often do not give the same answer. This might look something like:

Immediately, we see that one multiplication method produces a scalar and the other a vector, but if we carry on with our thought experiment and divide each side by A, I would get something like:

how can C be different than D, and yet have a division that produces the same result? It simply can’t.

Moreover, dividing something like direction by another direction doesn’t make much sense in the real world. We can half the velocity of an object by slowing it down, or we can half the distance an object travels, but what does it mean to divide a Northerly trajectory at 10 m/s by an Easterly trajectory at 3 m/s ? Not much. It mostly sounds like nonsense. Because it is.

References

[1] George Brown Arfken and Hans-Jurgen Weber. Mathematical methods for physicists. Academic Press, 1995.

[2] Mary L. Boas. Mathematical methods in the physical sciences. John Wiley Sons. New York, 1983.